https://cs231n.github.io/optimization-1/
CS231n Deep Learning for Computer Vision
Table of Contents: Introduction In the previous section we introduced two key components in context of the image classification task: A (parameterized) score function mapping the raw image pixels to class scores (e.g. a linear function) A loss function tha
cs231n.github.io
이번에는 위 내용에 대해서 한글로 정리해보겠습니다.
최적화(Optimization) 개요
최적화는 점수 함수, 손실 함수를 포함한 마지막 중요한 요소이다.
최적화란 손실 함수를 최소화하도록 매개변수 W를 찾는 과정이다.
손실 함수 시각화(Visualizing the Loss Function)
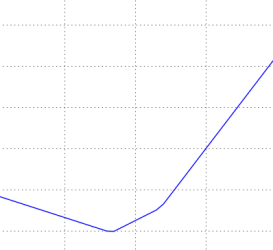
랜덤한 가중치 행렬 W에 대해서 하나 혹은 두 개의 임의의 가중치행렬을 이용하여 손실 함수를 시각화 할 수 있다.
L(W) -> L(W + a * W_1 ) : 한 방향 손실 함수 그래프
L(W) -> L(W + a * W_1 + b * W_2 ) : 두 방향 손실 함수 (이차원) 그래프


최적화 전략(Optimization Strategies)
다시 설명하자면 손실 함수는 특정 가중치 행렬 W의 품질 혹은 성능을 평가할 수 있게 한다.
최적화의 목표는 손실 함수를 최소화 시키는 W를 찾는 것이다.
그 W를 찾기 위해서 3가지 전략을 사용할 수 있다.
지금 여기서 설명에 사용될 SVM loss 같은 예시는 convex 문제에 해당되어 매우 간단하지만
결국 우리가 나중에 최적화할 대상은 인공신경망 같이 간단히 해결할 수 없는 문제이다.
- 전략 1: 랜덤 탐색(Random Search)
- 단순히 n번 반복하면서 계산한 loss가 최소일 때의 W를 저장하는 방식이다.
- 전략 2: 랜덤 국소 탐색(Random Local Search)
- 처음 W에서 loss가 감소하는 방향으로 조금씩 옮겨가면서 계산하는 방식이다.
- 전략 3: 기울기 추종(Following the Gradient / Gradient Descent)
- 기울기를 계산해서 loss의 최소값을 찾는 방식이다.
기울기 계산(Computing the Gradient)
기울기를 계산하는 방법에는 쉬운 방법인 수치적 기울기(numerical gradient)를 이용한 방법과
빠르고 정확하지만 에러가 발생하기 쉬운 해석적 기울기(analytical gradient)를 이용한 방법이 있다.
수치적 기울기는 유한 차분을 이용하며 해석적 기울기는 행렬 미분과 체인 룰을 사용한다.
경사 하강법(Gradient Descent) 세부사항
경사하강법에는 배치 경사하강법 (미니배치 경사하강법)과 확률적 경사하강법이 있다.
배치 경사하강법은 훈련 세트 전체에 대해 기울기를 계산하여 업데이트하고
확률적 경사하강법은 랜덤 샘플 1개에 대해 기울기를 계산해서 샘플당 여러번 업데이트한다.
학습률 스케줄링(learning rate scheduling)과 모멘텀(momentum) 등으로 수렴 속도 및 안정성을 개선할 수 있다.
'학습 > AI' 카테고리의 다른 글
| Deep Learning for Computer Vision : Neural Networks 1 (0) | 2025.04.27 |
|---|---|
| Deep Learning for Computer Vision : Backpropagation, Intuitions (0) | 2025.04.27 |
| Deep Learning for Computer Vision : Linear Classification (0) | 2025.04.25 |
| Deep Learning for Computer Vision : Image Classification (1) | 2025.04.23 |
| Ollama + deepseek 첫 질문이 너무 느릴 때 (0) | 2025.02.13 |