https://cs231n.github.io/neural-networks-1/
CS231n Deep Learning for Computer Vision
Table of Contents: Quick intro It is possible to introduce neural networks without appealing to brain analogies. In the section on linear classification we computed scores for different visual categories given the image using the formula \( s = W x \), whe
cs231n.github.io
이번에는 위 내용을 한글로 정리해보겠습니다.
빠른 소개 (Quick intro)
기존 선형 분류기에서 계산한 클래스 점수함수 s = W x를 확장하여
은닉층(hidden layer)과 비선형 활성화 함수를 도입한 신경망은 s = W_2 * max(0, W_1 * x )와 같은 형태로 표현할 수 있다.
max(0, - ) 함수가 비선형성을 나타내는 요소이고 제거했을 때 다시 선형함수가 된다.
그리고 그 비선형 활성화 함수가 모델의 표현력을 결정짓는 핵심이다.
파라미터 W1, W2는 확률적 경사 하강법(SGD)과 체인룰 기반 역전파(backpropagation)를 통해 학습한다.
단일 뉴런 모델 (Modeling one neuron)
뇌의 기본 계산 단위인 뉴런은 시냅스를 통해 입력 신호를 가중 합산(weighted sum)하고
일정 기준을 넘으면 스파이크(firing)를 발생시킨다.
이런 생물학적 사실을 바탕으로 수학적 모델을 만들어낸다.
수학적 모델은 입력 벡터 x와 가중치 w의 내적에 편향(bias) b를 더한 뒤 활성화 함수 f로 변환하여
출력 f(w^T *x + b)를 계산한다.
단일 뉴런을 선형 분류기로 활용 (Single neuron as a linear classifier)
단일 뉴런을 선형 분류기에 사용하는 예시로 시그모이드 함수가 있다.
두 개의 클래스가 있을 때 σ(∑_i (w_i * x_i) + b )의 의미를 확률 P(y_i = 1 | x_i; w ) 로 해석하고
다른 클래스일 확률을 P(y_i = 0 | x_i; w ) = 1 - P(y_i = 1 | x_i; w )로 해석할 수 있다.
그러면 교차 엔트로피 손실을 공식화 할 수 있고 이를 최적화하면 이진 소프트맥스 분류기가 만들어진다.
(Binary Softmax Classifier)
그 대신에 max-margin hinge loss를 뉴런의 결과물에 추가하면 이진 SVM으로도 활용할 수 있다.
정규화를 생물학적인 관점에서 바라본다면 시냅스 강도를 점진적으로 망각시키는 효과로 볼 수 있다.
주요 활성화 함수 (Common activation functions)
주요 활성화 함수에는 다음과 같이 있다.
- Sigmoid σ(x)=1/(1+e^{-x}): 출력 범위 [0,1], 기울기 소실(vanishing gradient) 및 비영(non-zero)-중심성 문제로 현재는 거의 사용되지 않음.
- Tanh: 출력 범위 [–1,1], zero-중심성을 갖추었으나 여전히 포화(saturation) 문제 존재.
- ReLU f(x)=max(0,x): 비포화 선형 형태로 SGD 수렴 속도를 크게 향상(예: 6배 이상)시키며 구현이 단순함.
하지만 ‘죽은 ReLU(dead neurons)’ 현상에 주의해야 함. - Leaky ReLU, PReLU: ReLU의 음수 구간 기울기를 작게 열어 활성화 문제를 완화.
- Maxout: max(w_1^T * x + b_1,w_2^T * x + b_2) 형태로 ReLU 계열을 일반화하나 파라미터 수가 두 배로 늘어남.
신경망 구조 (Neural Network architectures)
뉴런(unit)들을 비순환 그래프(DAG) 형태로 쌓아 레이어를 구성하며
가장 일반적인 레이어는 완전 연결층(fully-connected layer)이다.
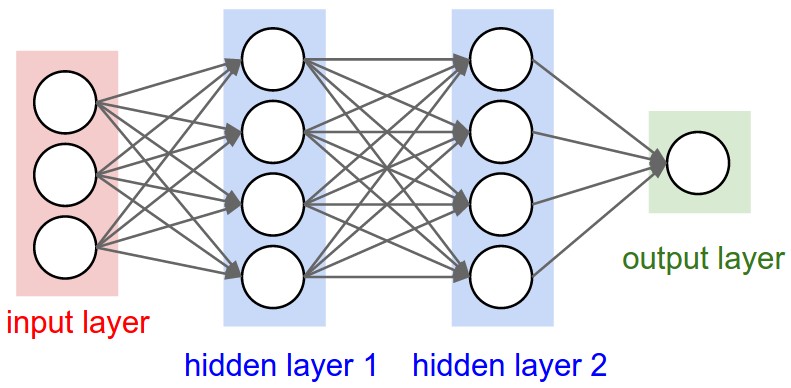
“N-layer” 네트워크는 숨겨진 층(hidden layers) 개수 N을 의미하며 입력층은 미포함으로 간주한다.
출력층(output layer)은 활성화 함수를 두지 않거나 선형(identity) 함수를 사용하여
회귀 혹은 클래스 점수를 바로 출력한다.
신경망의 크기는 흔히 학습가능한 파라미터 개수를 의미하며 가중치의 개수와 편향의 개수이다.
위의 그림의 경우에는 3*4 + 4*4 + 4*1 + 4 + 4 + 1 = 41 이다.
표현력 (Representational power)
하나의 은닉층만 있어도 연속 함수에 대한 보편 근사(universal approximation)가 가능하지만
실제로는 더 깊은 네트워크가 계층적(hierarchical) 특징을 효율적으로 학습하므로 성능이 우수하다.
레이어 및 크기 설정 (Setting number of layers and their sizes)
레이어 수·크기 증가 시 모델 용량(capacity)이 올라가 과적합 위험이 커지나
정규화(strength)(예: 가중치 감쇠, 드롭아웃)로 제어하는 것이 권장된다.
대형 네트워크는 초기화·학습 운에 덜 민감하고 다양한 해에 대해 성능 분산이 작다는 경험적 관측이 있다.
'학습 > AI' 카테고리의 다른 글
| Deep Learning for Computer Vision : Neural Networks 3 (1) | 2025.04.28 |
|---|---|
| Deep Learning for Computer Vision : Neural Networks 2 (0) | 2025.04.27 |
| Deep Learning for Computer Vision : Backpropagation, Intuitions (0) | 2025.04.27 |
| Deep Learning for Computer Vision : Optimization (0) | 2025.04.27 |
| Deep Learning for Computer Vision : Linear Classification (0) | 2025.04.25 |